The private key for a Comodo Code signing certificate is generated by the browser during certificate enrollment. When the submit button is pressed, a key pair of the selected size is generated. The private key is encrypted and stored in the local key database.

• Distributed Generation Systems
• Distributed Key Generation For The Internet Reviews
• Distributed Energy Generation
• Distributed Power Generation

Comodo recommends using Internet Explorer 8+ on Windows and Firefox on Mac for certificate enrollment as it is both easy to apply and convenient for the user. To apply for a Code signing certificate, visit the below URL.

BROWSER SUPPORT :

Jun 17, 2019  Distributed key generation. At a high-level, the DKG procedure creates a distributed secret key that is formed of n different key pairs (vki, ski), each one being held by the entity i in the system. These key pairs will eventually be used to instantiate a (t,n)-threshold signature scheme (we. Jun 26, 2019  The above-mentioned properties of BLS make it possible to implement Shamir’s Secret Sharing (SSS) and Distributed Key Generation (DKG). Shamir’s Secret Sharing is a threshold scheme that has been known for quite some time and proved its safety.

• What is the abbreviation for Distributed Key Generation? What does DKG stand for? DKG abbreviation stands for Distributed Key Generation.
• A distributed key generation (DKG) scheme overcomes these hurdles by removing the requirement of a dealer in secret sharing. A (threshold) DKG scheme achieves this using a complete distribution of the trust among a number of servers such that any subset of servers of size greater than a given threshold can reveal or use the shared secret, while.

1. Microsoft Internet Explorer: IE uses the CertEnroll/XEnroll ActiveX control to generate and install certificates through the browser.

Distributed Generation Systems

2. Mozilla Firefox: This browser supports key generation and certificate installation by default through the <keygen> function and special certificate file type handling.

Note: While Firefox supports in-browser certificate installation, it uses its own keystore to store the certificate and is not shared with other applications. Installing through Internet Explorer will install the certificate to the Windows Certificate Manager which is used by other applications such as Microsoft Office, Outlook, and Google Chrome. For this reason, Internet Explorer is recommended.

3. Microsoft Edge:Neither the <keygen> nor the CertEnroll/XEnroll ActiveX controls are present in Microsoft's new Edge browser.

4.Google Chrome: As of Chrome 49, the <keygen> function has been disabled by default and digital certificate file types are downloaded instead of installed. While the keygen function can manually be enabled, the custom filetype handling is still removed, therefore installation through Google Chrome is not supported.

ADDITIONAL INFORMATION:

Note: From Chromium Version 49, 'Key Generation' feature is no longer supported. So, please DO NOTuse any Chromium based browser for S/MIME certificate enrollment.

Some examples of Chromium Based browsers are, Google Chrome, Yandex Browser, Opera.

This cd key you get from us is unique.How to get Norton 360? Get the Norton 360 Generator! Norton 360 license key generator. Norton 360 CDKey Generator Generate Your Own KeyNorton 360 Serial Generator Generate Your Own Key.New Norton 360 CD-Key Generator online undetected. Hi everybody, and that’s why we decided to share with you Norton 360 Key Generator. This is the best version of Norton 360 CD-Key Generator.Norton 360 Cd key generator updated latest working tool online.Get Norton 360 Redeem Code Generator on PC, Xbox One, PS4, It is going to take time to generate unique Norton 360 redeem key.Norton 360 Key Generator.

In case you mistakenly used Chrome initially to apply for the certificate, then you must ignore the current certificate and go with the replacement option.

• If you are a direct customer of Comodo, Login to your account > Code Signing Certificates > 'Replace'. For this process, you must use Internet Explorer or Firefox just like we mentioned earlier.
• If you purchased this certificate from one of our re-sellers, then contact them for replacing your certificate.

Related Articles:

Distributed key generation (DKG) is a cryptographic process in which multiple parties contribute to the calculation of a shared public and private key set. Unlike most public key encryption models, distributed key generation does not rely on Trusted Third Parties.^[1] Instead, the participation of a threshold of honest parties determines whether a key pair can be computed successfully.^[2] Distributed key generation prevents single parties from having access to a private key. The involvement of many parties requires Distributed key generation to ensure secrecy in the presence of malicious contributions to the key calculation.^[1]

Distributed Key Generation is commonly used to decrypt shared ciphertexts or create group digital signatures.^[2]

History[edit]

Distributed key generation protocol was first specified by Torben Pedersen in 1991. This first model depended on the security of the Joint-Feldman Protocol for verifiable secret sharing during the secret sharing process.^[3]

In 1999, Rosario Gennaro, Stanislaw Jarecki, Hugo Krawczyk, and Tal Rabin produced a series of security proofs demonstrating that Feldman verifiable secret sharing was vulnerable to malicious contributions to Pedersen's distributed key generator that would leak information about the shared private key.^[4] The same group also proposed an updated distributed key generation scheme preventing malicious contributions from impacting the value of the private key.

Methods[edit]

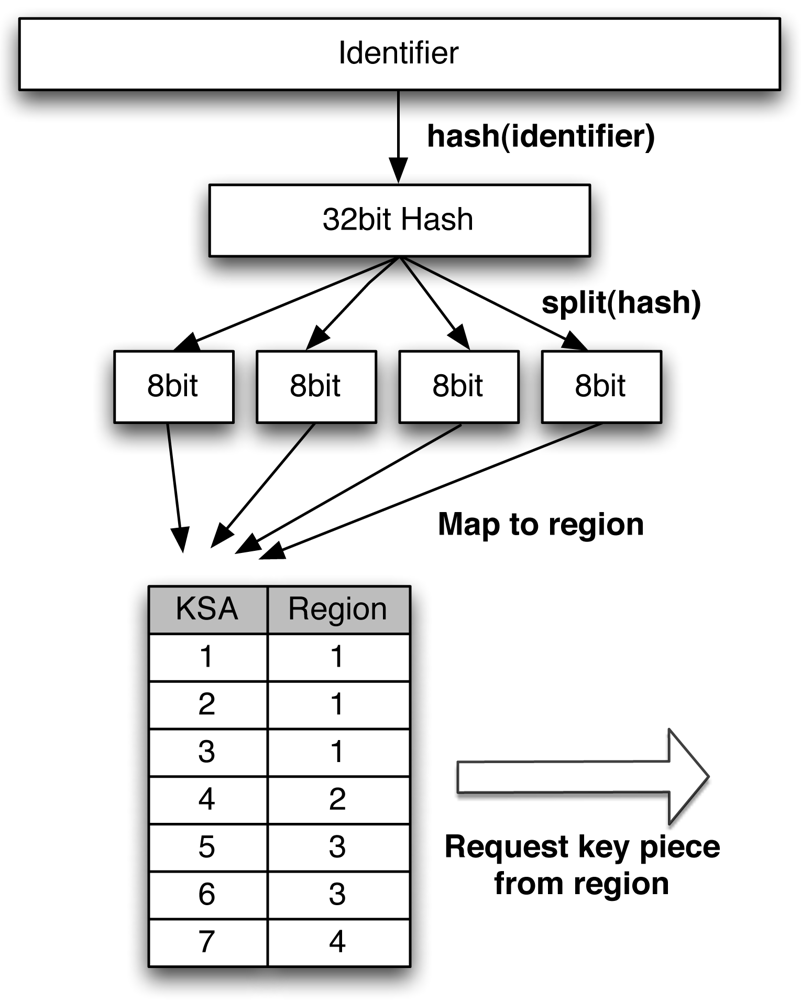
The distributed key generation protocol specified by Gennaro, Jarecki, Krawczyk, and Rabin assumes that a group of players has already been established by an honest party prior to the key generation. It also assumes the communication between parties is synchronous.^[4]

1. All parties use Pedersen's verifiable secret sharing protocol to share the results of two random polynomial functions.
2. Every party then verifies all the shares they received. If verification fails, the recipient broadcasts a complaint for the party whose share failed. Each accused party then broadcasts their shares. Each party then has the opportunity to verify the broadcast shares or disqualify accused parties. All parties generate a common list of non-disqualified parties.
3. Each non-disqualified party broadcasts a set of values constructed by raising a common generator to the power of each value used in one polynomial in Part 1.
4. These broadcast values are verified by each party similarly to as in Part 2. When a verification fails, the party now broadcasts both the values received in Part 1 and the values received in Part 3. For each party with verifiable complaints, all other parties reconstruct their own value sets in order to eliminate disqualified contributions.
5. The group computes the private key as the product of every qualified contribution (each qualified party's random polynomial evaluated at 0).^[4]

Avoiding the Synchrony Assumption[edit]

In 2009, Aniket Kate and Ian Goldberg presented a Distributed key generation protocol suitable for use over the Internet.^[5] Unlike earlier constructions, this protocol does not require a broadcast channel or the synchronous communication assumption, and a ready-to-use library is available.

Robustness[edit]

In many circumstances, a robust distributed key generator is necessary. Robust generator protocols can reconstruct public keys in order to remove malicious shares even if malicious parties still remain in the qualified group during the reconstruction phase.^[4] For example, robust multi-party digital signatures can tolerate a number of malicious users roughly proportionate to the length of the modulus used during key generation.^[6]

Sparse Evaluated DKG[edit]

Distributed key generators can implement a sparse evaluation matrix in order to improve efficiency during verification stages. Sparse evaluation can improve run time from ${\displaystyle O(nt)}$ (where ${\displaystyle n}$ is the number of parties and ${\displaystyle t}$ is the threshold of malicious users) to ${\displaystyle O(lo{g}^{3}n)}$. Instead of robust verification, sparse evaluation requires that a small set of the parties verify a small, randomly picked set of shares. This results in a small probability that the key generation will fail in the case that a large number of malicious shares are not chosen for verification.^[7]

Applications[edit]

Distributed key generation and distributed key cryptography are rarely applied over the internet because of the reliance on synchronous communication.^[4]

Distributed Key Generation For The Internet Reviews

Distributed key cryptography is useful in key escrow services where a company can meet a threshold to decrypt a ciphertext version of private key. This way a company can require multiple employees to recover a private key without giving the escrow service a plaintext copy.^[1]

Distributed key generation is also useful in server-side password authentication. If password hashes are stored on a single server, a breach in the server would result in all the password hashes being available for attackers to analyze offline. Variations of distributed key generation can authenticate user passwords across multiple servers and eliminate single points of failure.^[8][9]

Distributed key generation is more commonly used for group digital signatures. This acts as a form of voting, where a threshold of group members would have to participate in order for the group to digitally sign a document.^[2]

References[edit]

Distributed Energy Generation

1. ^ ^abcKate, Aniket; Goldberg, Ian (2010). Distributed Private-Key Generators for Identity Based Cryptography. Security and Cryptography for Networks. Lecture Notes in Computer Science. 6280. pp. 436–453. CiteSeerX10.1.1.389.4486. doi:10.1007/978-3-642-15317-4_27. ISBN978-3-642-15316-7.
2. ^ ^abcBoldyreva, Alexandra (2003). Threshold Signatures, Multisignatures and Blind Signatures Based on the Gap-Diffie-Hellman-Group Signature Scheme(PDF). Public Key Cryptography. Lecture Notes in Computer Science. 2567. pp. 31–46. doi:10.1007/3-540-36288-6_3. ISBN978-3-540-00324-3.
3. ^Pedersen, T. P. (1992). 'Non-Interactive and Information-Theoretic Secure Verifiable Secret Sharing'. Advances in Cryptology — CRYPTO '91. Lecture Notes in Computer Science. 576. pp. 129–140. doi:10.1007/3-540-46766-1_9. ISBN978-3-540-55188-1.
4. ^ ^abcdeGennaro, Rosario; Jarecki, Stanislaw; Krawczyk, Hugo; Rabin, Tal (24 May 2006). 'Secure Distributed Key Generation for Discrete-Log Based Cryptosystems'. Journal of Cryptology. 20 (1): 51–83. CiteSeerX10.1.1.134.6445. doi:10.1007/s00145-006-0347-3.
5. ^Kate, Aniket; Goldberg, Ian (2006). 'Distributed Key Generation for the Internet'. IEEE ICDCS. doi:10.1109/ICDCS.2009.21.
6. ^Castelluccia, Claude; Jarecki, Stanisław; Kim, Jihye; Tsudik, Gene (2006). 'Secure acknowledgment aggregation and multisignatures with limited robustness'. Computer Networks. 50 (10): 1639–1652. doi:10.1016/j.comnet.2005.09.021.
7. ^Canny, John; Sorkin, Steve (2004). Practical Large-scale Distributed Key Generation(PDF). Advances in Cryptography - EUROCRYPT 2004. Lecture Notes in Computer Science. 3027. pp. 138–152. CiteSeerX10.1.1.69.6028. doi:10.1007/978-3-540-24676-3_9. ISBN978-3-540-21935-4.
8. ^MacKenzie, Philip; Shrimpton, Thomas; Marcus, Jakobsson (2006). 'Threshold Password-authenticated Key Exchange'. Journal of Cryptology. 19 (1): 27–66. CiteSeerX10.1.1.101.6403. doi:10.1007/s00145-005-0232-5.
9. ^Jarecki, Stanislaw; Kiayias, Aggelos; Krawczyk, Hugo (2014). 'Round-Optimal Password-Protected Secret Sharing and T-PAKE in the Password-Only model'(PDF). Cryptology ePrint Archive. 650. Retrieved 5 November 2014.

Distributed Power Generation